Tri par arbre binaire
Principe
Avec cette méthode, on « voit » le tableau à trier comme un arbre binaire, c'est à dire une racine dont partent deux branches ; de chaque noeud partent deux branches, et ainsi de suite.La racine est constituée par la case n° 1 ; les autres cases se placent en séquence de gauche à droite, puis de haut en bas.
Exemple avec un tableau de 10 cases :
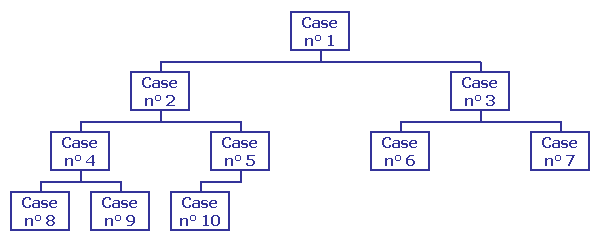
- Dans un premier temps, on fait en sorte que tout noeud contienne une valeur supérieure ou égale aux noeuds inférieurs
Dans l'exemple ci-dessus on doit avoir, par exemple :
contenu de la case n° 5 ≥ contenu de la case n° 10
contenu de la case n° 4 ≥ contenu des cases 8 et 9
contenu de la case n° 2 ≥ contenu des cases n° 4 et 5
etc ...
La valeur la plus élevée du tableau se trouve ainsi dans la racine de l'arbre, c'est à dire la case n° 1 - On échange le contenu de la case n° 1 (racine) et le contenu de la dernière case du tableau
La dernière case du tableau contient alors la valeur correcte par rapport au résultat final - En excluant la dernière case du tableau (correctement remplie), on réarrange l'arborescence selon les mêmes règles qu'à l'étape 1, puis on échange le contenu de la racine avec l'avant-dernière case du tableau.
- On répète ce processus, en éliminant la dernière case à chaque itération, jusqu'à ce qu'il ne reste plus d'arbre.
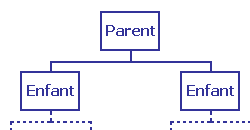
D'un noeud, que nous appellerons « Parent » peuvent partir au maximum deux branches aboutissant à des cases que nous appellerons « Enfants ».
Supposons dans un premier temps que toute l'arborescence située sous chacun des enfants est correctement agencée (chaque parent contient une valeur supérieure à chacun de ses enfants).
Deux cas peuvent se produire :
- Le contenu du parent est supérieur ou égal au contenu de chacun des enfants
Dans ce cas, toute l'arborescence de « Parent » est correcte, et il n'y a rien à faire - Le contenu d'au moins un des enfants est supérieur au contenu du parent
On échange le contenu du parent avec l'enfant ayant le plus grand contenu, mais il faut alors s'assurer que l'enfant en question a bien un contenu supérieur ou égal au contenu de ses propres enfants : il suffit pour cela de considérer que l'enfant en question est maintenant un parent et d'effectuer les mêmes opérations que précédemment. - On répète le processus jusqu'au niveau le plus bas de l'arborescence
En fait, il n'est pas nécessaire d'effectuer un échange à chaque étape : il suffit de mémoriser le contenu du parent initial, d'effectuer tous les tests par rapport à ce contenu : la dernière case libérée devra accueillir cette valeur.
L'hypothèse prise est toujours respectée après la première itération, puisque seule la racine peut être déclassée (contenu échangé avec la dernière case du tableau).
Seul le cas de l'étape 1 reste donc à règler.
Pour obtenir un arbre correct à la fin de l'étape 1 :
- On traite les parents situés le plus bas dans l'arbre (c'est à dire ceux dont les enfants n'ont pas d'enfant) selon le processus précédent
- On remonte ensuite d'un niveau, et on traite tous les parents selon le même processus (l'hypothèse est respectée), et ainsi de suite jusqu'à la racine.
Algorithme
Pour tout élément I, depuis le milieu du tableau en remontant vers le début- Créer un arbre en prenant l'élément I comme parent
- Pour tout élément I, depuis la fin du tableau en remontant vers le 1er élément
- Echanger l'élément I avec le 1er élément du tableau
- Créer un arbre en prenant le 1er élément comme parent
Pour créer un arbre :
Mémoriser le contenu initial du ParentEnfant = Position du 1er enfant
Tant que la position de l'Enfant est dans le tableau
- S'il existe un 2ème enfant
- Positionner Enfant sur celui des 2 enfants ayant le plus grand contenu
- Si le contenu initial du Parent est supérieur au contenu de l'Enfant
- Fin tant que
- Sinon
- Copier le contenu de Enfant dans Parent
- Positionner le nouveau Parent sur Enfant
- Enfant = Position de son 1er enfant
Copier dans la position courante de Parent le contenu initial du Parent
Exemple
Tableau à trier : [7,5,1,9,2]
Le n° déchelon du tableau est indiqué en rouge.
Construction de l'arbre initial |
||
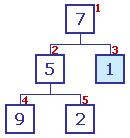 Etat initial de l'arbre non ordonné. Etat initial de l'arbre non ordonné.
L'échelon n° 3 (contenant la valeur 1), pris comme parent, n'a pas d'enfant ; sa descendance est donc correcte. |
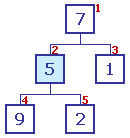 L'échelon n° 2 (contenant 5) est parent. L'échelon n° 2 (contenant 5) est parent.
Ses enfants sont comparés ; le plus grand contient 9. |
|
|
|
||
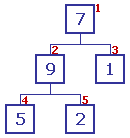 Puisque 9 > 5, les contenus sont échangés. Puisque 9 > 5, les contenus sont échangés.
Il n'y a plus de descendance. |
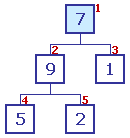 L'échelon n° 1 (contenant 7) est parent. L'échelon n° 1 (contenant 7) est parent.
Ses enfants sont comparés ; le plus grand contient 9. |
|
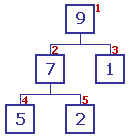 Puisque 9 > 7, les contenus sont échangés Puisque 9 > 7, les contenus sont échangés
Un échange ayant eu lieu, on examine la descendance à partir de l'enfant avec lequel s'est effectué l'échange. L'échelon n° 2 (contenant 7) est parent. Ses enfants sont comparés ; le plus grand contient 5 Puisque 7 > 5, les contenus sont ordonnés ; l'arbre reste inchangé Puisqu'on est parti de la racine, l'arbre est ordonné |
||
1ère itération |
||
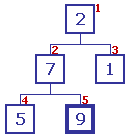 Le contenu du premier et du dernier échelon sont échangés. Le contenu du premier et du dernier échelon sont échangés.
Le dernier échelon contient maintenant sa valeur finale, et est exclu du reste du traitement |
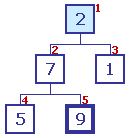 L'échelon n° 1 (contenant 2) est parent L'échelon n° 1 (contenant 2) est parent
Ses enfants sont comparés ; le plus grand contient 7 |
|
|
|
||
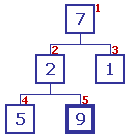 Puisque 7 > 2, les contenus sont échangés Puisque 7 > 2, les contenus sont échangés
Un échange ayant eu lieu, on examine la descendance à partir de l'enfant avec lequel s'est effectué l'échange. |
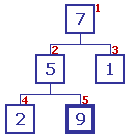 Puisque 5 > 2, les contenus sont échangés Puisque 5 > 2, les contenus sont échangés
Il n'y a plus de descendance, l'arbre restant est donc ordonné |
|
2ème itération
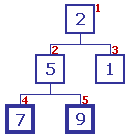 Le contenu du premier et du dernier échelon sont échangés Le contenu du premier et du dernier échelon sont échangés
Le dernier échelon contient maintenant sa valeur finale, et est exclu du reste du traitement |
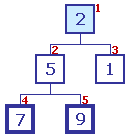 L'échelon n° 1 (contenant 2) est parent L'échelon n° 1 (contenant 2) est parent
Ses enfants sont comparés ; le plus grand contient 5 |
|
|
|
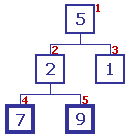 Puisque 5 > 2, les contenus sont échangés Puisque 5 > 2, les contenus sont échangés
Il n'y a plus de descendance, l'arbre restant est donc ordonné |
|
3ème itération |
|
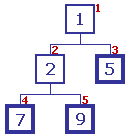 Le contenu du premier et du dernier échelon sont échangés Le contenu du premier et du dernier échelon sont échangés
Le dernier échelon contient maintenant sa valeur finale, et est exclu du reste du traitement |
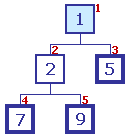 L'échelon n° 1 (contenant 1) est parent L'échelon n° 1 (contenant 1) est parent
Un seul de ses enfants est à prendre en compte ; il contient 2 Il ne reste donc plus que ces 2 cases. Puisqu'elles sont ordonnées, le tri est terminé Voir remarque ci-après. |
Pour appliquer strictement l'algorithme, il faudrait ordonner le dernier arbre constitué des cases 1 et 2, ce qui conduirait à échanger leur contenu, puis démarrer une itération et les échangeant de nouveau.
Exemple de programme en Visual Basic
Remarques
- La deuxième moitié du tableau ne contient jamais de parent ; dans un tableau à N éléments, les parents seront tous entre 1 et N/2
- Si on appelle :
I Min = indice (n° de case) du premier échelon du tableau
I Parent = indice d'un parent
L'indice de son premier enfant est donné par :
I Enfant = (2 * I Parent ) - I Min + 1
Pour l'indice du deuxième enfant éventuel, il suffit d'ajouter 1 à la valeur précédente.
Utilisation
Cet algorithme est généralement assez performant mais, en moyenne, moins que le tri rapide.Par contre les performances sont relativement indépendantes de la répartition initiale des valeurs ; c'est donc un algorithme intéressant s'il n'y a pas de tendance particulière à cette répartition.
Retour à la table des matières des tris
Dernière mise à jour de cette page : 12/8/2007